Abstract
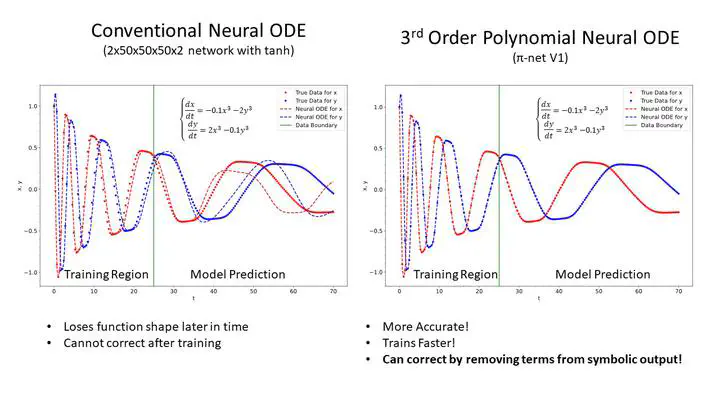
Neural networks have the ability to serve as universal function approximators, but they are not interpretable and do not generalize well outside of their training region. Both of these issues are problematic when trying to apply standard neural ordinary differential equations (ODEs) to dynamical systems. We introduce the polynomial neural ODE, which is a deep polynomial neural network inside of the neural ODE framework. We demonstrate the capability of polynomial neural ODEs to predict outside of the training region, as well as to perform direct symbolic regression without using additional tools such as SINDy.
Add the publication’s full text or supplementary notes here. You can use rich formatting such as including code, math, and images.
Colby Fronk
AI4Science PhD Student
My research interests include multidisciplinary scientific computing and AI4Science.